선형 회귀는 훈련 데이터의 훈련 샘플에 가장 잘 맞는 직선을 찾는 것으로 이해할 수 있다.
최소 제곱법(Ordinary Least Squares, OLS), 선형 최소 제곱법(Linear Least Squares)
훈련 샘플까지 수직 거리(잔차 또는 오차)의 제곱합을 최소화하는 선형 회귀 직선의 모델 파라미터를 추정하는 방법이다.
(SVM은 마진을 최대화 하는 모델 파라미터를 추정하는 방법이였다.)
find regression parameter with Gradient Descent,GD & Stochastic Gradient Descent
아달린(Adaline)의 비용함수 J(w)는 제곱 오차합(Sum of Squared Errors, SSE)으로 OLS에서와 같다.
즉, OLS는 단위 계단 함수가 없는 아달린으로 해석할 수 있다.
클래스 레이블 -1 이나 1 대신 연속적인 타깃 값을 얻는다.
class LinearRegressionGD(object):
def __init__(self, eta=0.001, n_iter=20):
self.eta=eta
self.n_iter=n_iter
def fit(self, X, y):
self.w_=np.zeros(1+X.shape[1])
self.cost_=[]
for i in range(self.n_iter):
output=self.net_input(X)
errors=(y-output)
self.w_[1:]+=self.eta*X.T.dot(errors)
self.w_[0]+=self.eta*errors.sum()
cost=(errors**2).sum()/2.0
self.cost_.append(cost)
return self
def net_input(self, X):
return np.dot(X, self.w_[1:])+self.w_[0]
def predict(self, X):
return self.net_input(X)
RM(방 개수) 변수를 특성으로 사용하여 MEDV(주택 가격)을 예측
X=df[['RM']].values
y=df['MEDV'].values
from sklearn.preprocessing import StandardScaler
sc_x=StandardScaler()
sc_y=StandardScaler()
X_std=sc_x.fit_transform(X)
y_std=sc_y.fit_transform(y[: ,np.newaxis]).flatten()
lr=LinearRegressionGD()
lr.fit(X_std, y_std)
import matplotlib.pyplot as plt
plt.plot(range(1, lr.n_iter+1), lr.cost_)
plt.ylabel('SSE')
plt.xlabel('Epoch')
plt.show()
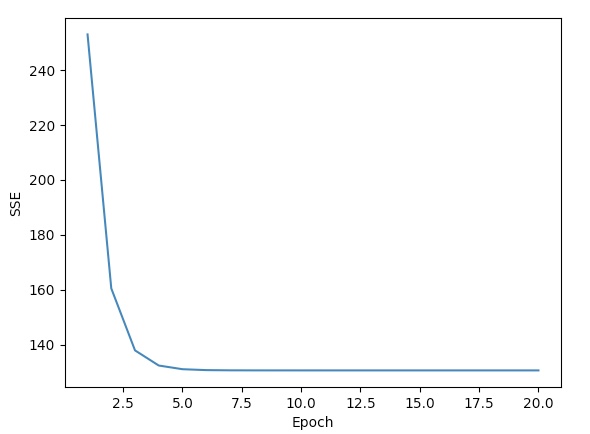
경사 하강법 알고리즘은 약 다섯 번째 에포크에서 수렴한다. y axis는 Sum of Squared Errors
회귀 곡선(Regression Line)
import matplotlib.pyplot as plt
def lin_regplot(X, y, model):
plt.scatter(X, y, c='steelblue', edgecolor='white', s=70)
plt.plot(X, model.predict(X), color='black', lw=2)
return None
lin_regplot(X_std, y_std, lr)
plt.xlabel('Average number of rooms [RM] (standardized)')
plt.ylabel('Price in $1000s [MEDV] (standardized)')
plt.show()
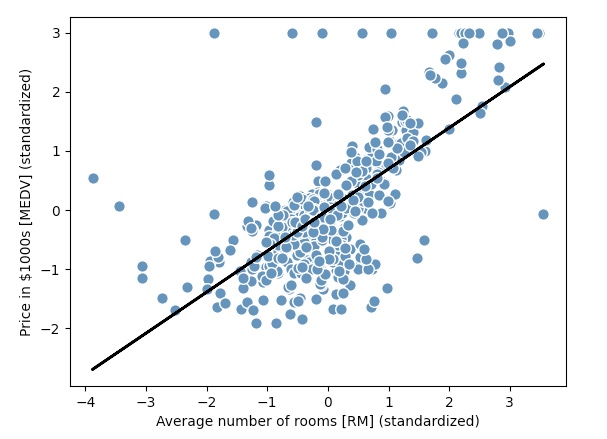
위 그래프는 방 개수가 주택 가격을 잘 설명하지 못하는 경우도 많다는 것을 알려 준다.
y=3에서 다수의 데이터 포인트가 늘어서 있는 것을 볼 수 있다.
이는 초과되는 가격을 잘라 냈다는 것을 의미한다.
어떤 애플리케이션에서는 예측된 출력값을 원본 스케일로 복원하여 제공해야 한다.
sc_y.inver_transform(price_std)
5개 방을 가진 주택 가격을 예측
num_rooms_std=sc_x.transform(np.array([[5.0]]))
price_std=lr.predict(num_rooms_std)
print("$1,000 단위 가격: %.3f" %sc_y.inverse_transform(price_std))
$1,000 단위 가격: 10.840
print('기울기: %.3f' %lr.w_[1])
print('절편: %.3f' %lr.w_[0])
기울기: 0.695
절편: -0.000
표준화 처리된 변수를 사용할 때 기술적으로 절편을 업데이트할 필요가 없다.
y축 절편이 항상 0이기 때문이다.(타깃 데이터 y도 표준화 했기 때문에)
모델 성능에 영향을 미치지 않기 때문에 일반적으로 타깃 값은 표준화 하지 않는다.
Scikit-learn Linear Regression fit
scikitlearn의 추정기는 SciPy 최소 제곱 구현(scipy.linalg.lstsq)을 사용한다.
이 함수는 선형 대수학 패기키(LAPACK)에 기반한 매우 최적화된 코드를 사용한다.
사이킷런의 선형 회귀 구현은 표준화하지 않은 특성에서 (더) 잘 동작한다.
경사 하강법 기반의 최적화를 사용하지 않기 때문에 표준화 전처리 단계를 건너뛸 수 있다.
from sklearn.linear_model import LinearRegression
slr=LinearRegression()
slr.fit(X, y)
print('기울기: %.3f' %slr.coef_[0])
print('절편: %.3f' %slr.intercept_)
기울기: 9.102
절편: -34.671
lin_regplot(X, y, slr)
plt.xlabel('Average number of rooms [RM]')
plt.ylabel('Price in $1000s [MEDV]')
plt.show()

표준화한 데이터와 모델의 가중치가 달라졌지만, RM에 대한 MEDV 그래프를 그려서 직접 만든 경사 하강법 구현과 비교 해보면,
데이터를 비슷하게 잘 학습했다는 것을 알 수 있다.
Solution of OLS with System of linear equation(연립 일차 방정식): 정규 방정식(normal equation)
Xb=np.hstack((np.ones((X.shape[0], 1)), X))
w=np.zeros(X.shape[1])
z=np.linalg.inv(np.dot(Xb.T, Xb))
w=np.dot(z, np.dot(Xb.T, y))
print('기울기: %.3f' %w[1])
print('절편: %.3f' %w[0])
기울기: 9.102
절편: -34.671
위 방법은 해석적으로 최적의 해를 찾는 것을 보장한다.
하지만 매우 큰 데이터셋을 다룬다면 이 (정규 방정식) 공식에 있는 역행렬을 구할 때 계산 비용이 너무 많이 든다.
또한 훈련 샘플을 담는 행렬이 특이 행렬(singular matrix, 비가역 행렬)일 수 있다.
따라서 반복적인 방법이 선호된다.
경사하강법, 확률적 경사 하강법, 정규 방정식, QR 분해, 특이 값 분해를 사용한 선형 회귀를 비교하고 싶다면, MLxtend에 구현된
LinearRegression 클래스를 사용할 수 있다.
Singular Matrix
역행렬이 존재하지 않는 행렬
QR 분해
QR분해는 실수 행렬을 직교 행렬(orthogonal matrix) Q와 상삼각 행렬(upper triangular matrix) R의 곱으로
표현하는 행렬 분해 방법이다.
w=(R^-2)(Q^T)y
Q, R=np.linalg.qr(Xb)
w=np.dot(np.linalg.inv(R), np.dot(Q.T, y))
print('기울기: %.3f' %w[1])
print('절편: %.3f' %w[0])
기울기: 9.102
절편: -34.671
LinearRegression scipy.linalg.lstsq
유사역행렬(pseudo-inverse matrix)
머신러닝교과서with파이썬,사이킷런,텐서플로_개정3판pg.418
w=np.dot(np.linalg.pinv(Xb), y)
print('기울기: %.3f' %w[1])
print('절편: %.3f' %w[0])
기울기: 9.102
절편: -34.671